5.7 Logit og probit - logistisk regresjonsanalyse
Logistisk regresjonsanalyse brukes til å beregne sannsynligheten for «suksess» (én tilstand foran en annen) eller for å havne i en av flere mulige tilstander.
Syntax:
logit <variabel> <variabelliste> [if <betingelse>] [,<opsjoner>]
probit <variabel> <variabelliste> [if <betingelse>] [,<opsjoner>]
Den avhengige variabelen må angis først, etterfulgt av forklaringsvariablene. Opsjoner kan benyttes for ulike formål, som f.eks. robust- eller cluster-estimering, jfr. underkapitlene nedenfor. I likhet med andre statistiske kommandoer, kan også regresjonskommandoer kombineres med en if-betingelse for å kjøre regresjoner på utvalgte grupper. For full oversikt over muligheter, bruk kommandoen help logit eller help probit.
Kommandoene logit og probit brukes til å utføre en logistisk analyse der den avhengige variabelen er en kategorisk variabel med 2 mulige utfall (dummyvariabel). Eksempler kan være jobb/ikke jobb, alderspensjonist/ikke pensjonert etc. Logit-modeller antar at
sannsynligheten for «suksess» følger en logaritmisk (log) fordeling, mens probit-varianten antar en normalfordeling. De to fordelingene er tilnærmet like, og resultatene vil derfor bli tilnærmet like. Logit er imidlertid den mest brukte modellen, og det er den vi fokuserer på i eksemplene nedenfor.
Resultatet av kommandoen logit gir en tabell med standardverdier som koeffisienter, standardavvik, z-verdier, p-verdier og konfidensintervall. Tallene inni hovedtabellen knyttes til de ulike variablene, mens tallene øverst viser til analysemodellen som helhet (gir pekepinn på modellens kvalitet/forklaringskraft).
Eksempel:
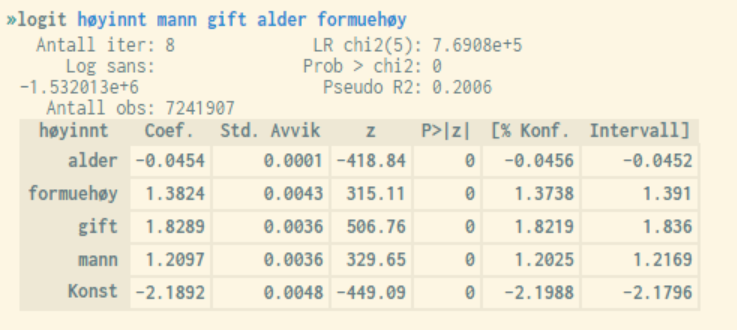
I eksempelet over er den avhengige variabelen høyinnt kodet på følgende måte:
generate høyinnt = 0
replace høyinnt = 1 if innt05 > 400000
Faktorvariabler, og cluster- og robust-estimering kan også benyttes. Fremgangsmåten er den samme som for ordinær lineær regresjon. Se hhv. kapittel 5.4.1 og 5.4.3 for mer informasjon om dette.
I likhet med ordinær lineær regresjonsanalyse (se kapittel 5.4) er det noen tall som er viktigere å se på enn andre. P-verdien "Prob > chi2" angir hvor god modellen er, dvs. den angir hvor stor forklaringskraft summen av alle variablene i modellen har. Jo nærmere 0 dess bedre, og verdier bør være under 0.05.
Pseudo R2 er en variant av Justert (rapporteres ved ordinære lineære regresjonsanalyser) som angir hvor stor andel av variansen i responsvariabelen som blir forklart av de uavhengige variablene (skala fra 0 til 1 der en søker høyest mulig verdi). Dette samlemålet må imidlertid tolkes med stor grad av varsomhet ettersom den i mange tilfeller angir en verdi som enten er kunstig høy eller lav. "Prob > chi2" er derfor å anbefale for logistiske regresjonsmodeller.
Variablenes p-verdi "P > |z|" tilsvarer "P > |t|" i ordinær lineær regresjonsanalyse. Grenseverdien er også her 0.05 om en opererer med et signifikansnivå på 5% (noe de fleste bruker). Rapporterte verdier under dette gjør at en kan konkludere med at tilhørende variabel er signifikant på et 5% nivå.
Det er det samme om en ser på z-verdi eller tilhørende p-verdi. Verdien z er en standardisert versjon av coeffisientverdien, som har forventning lik 0 og der verdier som overstiger +/- 1.96 impliserer at den aktuelle variabelen som koeffisienten tilhører har en signifikant påvirkning på sannsynligheten for «suksess». Positive verdier angir positiv effekt, og vice versa.
Konfidensintervallet gitt ved de to kolonnene lengst til høyre kan tolkes på samme måte som for ordinær lineær regresjonsanalyse, dvs. om det inkluderer verdien 0 tyder dette på null signifikans.
En ser av eksempelet ovenfor at alle forklaringsvariablene er signifikante med god margin (har høye z-verdier). "Alder" har en negativ effekt på sannsynligheten for å havne i en høyinntektsgruppe, mens de andre variablene har en tilsvarende positiv effekt. Videre ser en at modellens P-verdi er lik 0, noe som viser at vi har en god forklaringsmodell.